Cooperation Among Humans
Cooperation in Humans Game Theory Prisoner´s Dilemma & Social Dilemmas Philosophical Approach
Prisoner´s Dilemma & Social Dilemmas
This image can be freely used provided that credit is given to this web site.
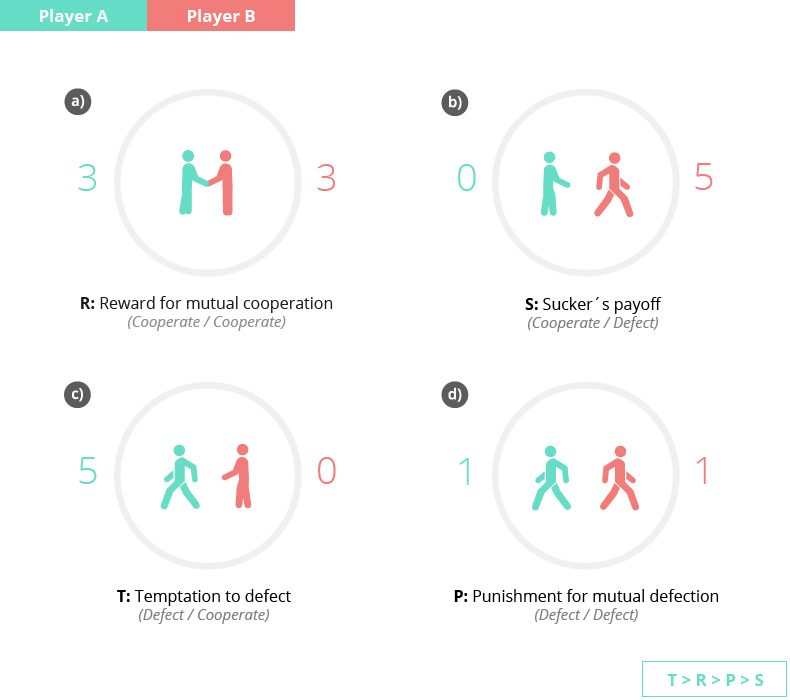
- Unilateral defection provides the highest payoff for the defector (player B in panel b or player A in panel c).
- Unilateral cooperation results in the lowest payoff for the cooperator (player A in panel b or player B in panel c).
- Nevertheless, in terms of collective payoffs, mutual cooperation reports the highest payoff, as it results in a payoff of 3 for each cooperator, so the total amount is 3+3=6. (See panel a).
- On the contrary, mutual defection gives the lowest payoff, i.e., 1+1=2, (See panel d). The benefits obtained when both prisoners confess (betray each other) is less than the benefit they would have obtained if both would have remained silent (cooperate).
The dilemma then comes from the fact that from an individual perspective, the best course of action is to defect, because whatever your opponent does, you will never earn less than her (5 and 0 if you defect and your opponent cooperate; or 1 and 1 if both defect). But, in a fully rational population, everybody will think in the same way, and all players will end up playing as defectors. However, mutual cooperation would have led to maximizing social welfare.
From an individual perspective, not cooperating is always the best strategy:
- If the other player cooperated, I would earn more benefits if I did not.
- If the other player did not cooperate, the best thing for me would be not cooperating either.
However, mutual cooperation is better than not cooperating unilaterally. That is the dilemma!

Collective Social Dilemmas
There is a group of 6 individuals, each one with 10 Euros.
In each round of the game, each individual can contribute to the public good with any amount between 0 and 10 Euros. At the end, the bank will triple (x3) the amount collected from all and divide it among the group members.
Individually, the best option is to contribute nothing, because if the other participants do not cooperate, every euro would generate only 0.5 Euros (3×1/6). Nevertheless, the best collective strategy would be that each participant provides an amount of 10 Euros, because so the profit would be the maximum for everyone: 3x10x6/6 = 30 Euros.
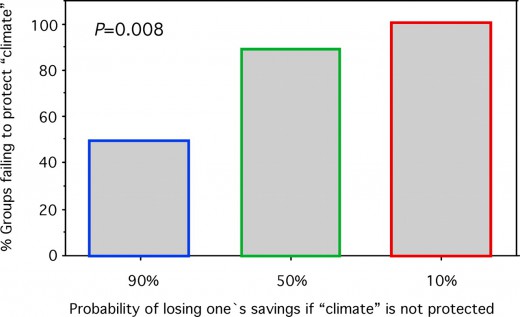
There is a group of 6 individuals involved in this experiment that should achieve a common goal: contribute to the prevention of climate change.
Each individual begins the game with 40 Euros. They must play a total of 10 rounds and in each round; everyone can contribute to the public good with the following amounts: 0, 2, or 4 Euros.
If at the end of the game, a minimum amount of 120 Euros is collected among all the individuals, the common goal will be reached and therefore, everyone may keep the savings. Otherwise, they can lose everything saved with a given probability. (See figure below).