Evolutionary Game Theory
E. Artiges, C. Gracia-Lazaro, L. M. Floria, and Y. Moreno, «Replicator population dynamics of group (n-agent) interactions. Broken symmetry, thresholds for metastability and macroscopic behavior», Physical Review E 100, 052307 (2019).
Jose A. Cuesta, Carlos Gracia-Lázaro, Yamir Moreno, and Angel Sánchez, «Reputation is required for cooperation to emerge in dynamic networks», Comment to: Melamed, D., Harrell, A., Simpson, B. (2018). Cooperation, clustering, and assortative mixing in dynamic networks. Proc Natl Acad Sci USA, 201715357. Archived March 2018 .
W. Chen, C. Gracia-Lazaro, Z. Li, L. Wang, and Y. Moreno, «Evolutionary dynamics of N-person Hawk-Dove games», Scientific Reports 7:4800 (2017).
S. Meloni, C. Xia and Y. Moreno, «Heterogeneous resource allocation can change social hierarchy in public goods games», Royal Society Open Science 4:170092 (2017).
C. Gracia-Lazaro, L. M. Floria, and Y. Moreno, «Cognitive Hierarchy Theory and Two-person Games», Games 8(1), 1-18 (2017).
A. Aleta, S. Meloni, M. Perc, and Y. Moreno, «From degree-correlated to payoff-correlated activity for an optimal resolution of social dilemmas», Physical Review E 94, 062315 (2016).
C.-Y. Xia, S. Meloni, M. Perc and Y. Moreno, «Dynamic instability of cooperation due to diverse activity patterns in evolutionary social dilemmas», Europhysics Letters 109, 58002 (2015).
C. Gracia-Lázaro, L. M. Floría, J. Gómez-Gardeñes and Y. Moreno, “Cooperation in changing environments: Irreversibility in the transition to cooperation in complex networks“, Chaos, Solitons and Fractals 56, 188 (2013).
Z. Wang, C.-Y. Xia, S. Meloni, C.-S. Zhou and Y. Moreno, ”Impact of social punishment on cooperative behavior in complex networks“, Scientific Reports 3, 3055 (2013).
M. Perc, J. Gómez-Gardeñes, A. Szolnoki, L. M. Floría and Y. Moreno, “Evolutionary dynamics of group interactions on structured populations – A review“, Journal of the Royal Society Interface 10, 20120997 (2013).
Figure of the section: “Accounting for group structure: bipartite graphs”.
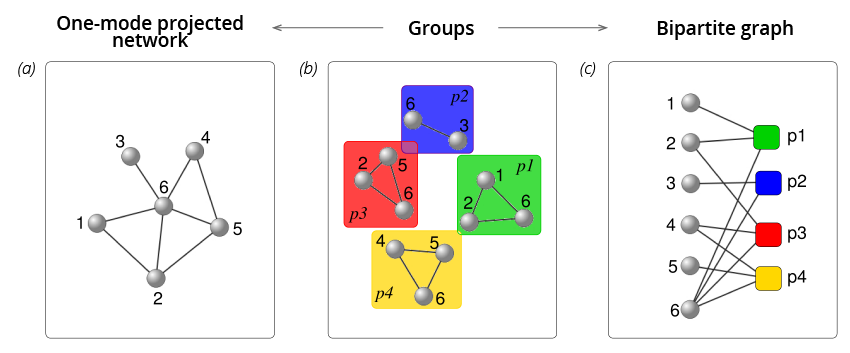
Schematic display of the two different forms of encoding collaboration data. In the central plot (b), several collaborating groups represent the original data. The interactions among players can be translated into a projected complex network (a). However, if one aims at preserving all the information about the group structure, a representation as a bipartite graph (c) is more appropriate. Jaime Iranzo, Mario Floría, Yamir Moreno and Angel Sánchez, “Empathy emerges spontaneously in the ultimatum game: Small groups and networks”, PLOS One 7(9), e43781 (2012). J. Gómez-Gardeñes, C. Gracia-Lázaro, L. M. Floría and Y. Moreno, “Evolutionary Dynamics on Interdependent Networks”, Physical Review E 86, 056113 (2012). C. Xia, S. Meloni, and Y. Moreno, “Effects of environment knowledge on agglomeration and cooperation in spatial Public Goods Games“, Advances in Complex Systems 15, 1250056 (2012). A. Cardillo, S. Meloni, J. Gómez-Gardeñes, and Y. Moreno, “Velocity-enhanced Cooperation of Moving Agents playing Public Goods Games“, Physical Review E 85, 067101 (2012). J. Poncela, J. Gomez-Gardeñes, L. M. Floría, and Y. Moreno, “Growing Networks Driven by the Evolutionary Prisoner’s Dilemma Game”. Chapter contribution to the Handbook of Optimization in Complex Networks, Springer Optimization and Its Applications, Vol. 57, Thai, My T.; Pardalos, Panos M. (Eds.) 2012. Jelena Grujic, José A. Cuesta y Angel Sánchez, “On the coexistence of cooperators, defectors and conditional cooperators in the multiplayer iterated Prisoner’s Dilemma”, Journal of Theoretical Biology 300, 299-308 (2012). Carlos P. Roca, Angel Sánchez y José A. Cuesta, “Individual strategy update and emergence of cooperation in social networks”, Journal of Mathematical Sociology 36, 1 (2012). Michele Starnini, Angel Sánchez, Julia Poncela and Yamir Moreno, “Coordination and growth: The Stag Hunt game on evolutionary networks”, Journal of Statistical Mechanics: Theory and Experiment, P05008 (2011) . Carlos P. Roca, José A. Cuesta y Angel Sánchez, “ Evolutionary game theory: temporal and spatial effects beyond replicator dynamics” Physics of Life Reviews 6, 208-249 (2009).
J. Poncela, J. Gómez-Gardeñes, A. Traulsen, and Y. Moreno, “Evolutionary Game Dynamics in a Growing Structured Population“,
New Journal of Physics, 11, 083031 (2009). Open access to the Journal or PDF Version.
Carlos P. Roca, José A. Cuesta y Angel Sánchez, “Imperfect imitation can enhance cooperation”,
EPL 87, 48005 (2009).
J. Gómez-Gardeñes, J. Poncela, L. M. Floría, and Y. Moreno,”Natural Selection of cooperation and degree hierarchy in heterogeneous populations“, Journal of Theoretical Biology 253, 296 (2008).
Julia Poncela, Jesús Gómez Gardeñes, Luis M. Floría, Angel Sánchez y Yamir Moreno, “Complex cooperative networks from evolutionary preferential attachment “, PLoS ONE 3(6): e2449 (2008).
J. Gómez-Gardeñes, M. Campillo, L. M. Floría, and Y. Moreno, “Dynamical Organization of Cooperation in Complex Topologies“, Physical Review Letters 98, 108103 (2007).
Abstract
Interactions among living organisms, from bacteria colonies to human societies, are inherently more complex than interactions among particles and non-living matter. Group interactions are a particularly important and widespread class, representative of which is the public goods game. In addition, methods of statistical physics have proved valuable for studying pattern formation, equilibrium selection and self-organization in evolutionary games. Here, we review recent advances in the study of evolutionary dynamics of group interactions on top of structured populations, including lattices, complex networks and co-evolutionary models. We also compare these results with those obtained on well-mixed populations. The review particularly highlights that the study of the dynamics of group interactions, like several other important equilibrium and non-equilibrium dynamical processes in biological, economical and social sciences, benefits from the synergy between statistical physics, network science and evolutionary game theory.

Schematic display of the two different forms of encoding collaboration data. In the central plot (b), several collaborating groups represent the original data. The interactions among players can be translated into a projected complex network (a). However, if one aims at preserving all the information about the group structure, a representation as a bipartite graph (c) is more appropriate. Jaime Iranzo, Mario Floría, Yamir Moreno and Angel Sánchez, “Empathy emerges spontaneously in the ultimatum game: Small groups and networks”, PLOS One 7(9), e43781 (2012). J. Gómez-Gardeñes, C. Gracia-Lázaro, L. M. Floría and Y. Moreno, “Evolutionary Dynamics on Interdependent Networks”, Physical Review E 86, 056113 (2012). C. Xia, S. Meloni, and Y. Moreno, “Effects of environment knowledge on agglomeration and cooperation in spatial Public Goods Games“, Advances in Complex Systems 15, 1250056 (2012). A. Cardillo, S. Meloni, J. Gómez-Gardeñes, and Y. Moreno, “Velocity-enhanced Cooperation of Moving Agents playing Public Goods Games“, Physical Review E 85, 067101 (2012). J. Poncela, J. Gomez-Gardeñes, L. M. Floría, and Y. Moreno, “Growing Networks Driven by the Evolutionary Prisoner’s Dilemma Game”. Chapter contribution to the Handbook of Optimization in Complex Networks, Springer Optimization and Its Applications, Vol. 57, Thai, My T.; Pardalos, Panos M. (Eds.) 2012. Jelena Grujic, José A. Cuesta y Angel Sánchez, “On the coexistence of cooperators, defectors and conditional cooperators in the multiplayer iterated Prisoner’s Dilemma”, Journal of Theoretical Biology 300, 299-308 (2012). Carlos P. Roca, Angel Sánchez y José A. Cuesta, “Individual strategy update and emergence of cooperation in social networks”, Journal of Mathematical Sociology 36, 1 (2012). Michele Starnini, Angel Sánchez, Julia Poncela and Yamir Moreno, “Coordination and growth: The Stag Hunt game on evolutionary networks”, Journal of Statistical Mechanics: Theory and Experiment, P05008 (2011) . Carlos P. Roca, José A. Cuesta y Angel Sánchez, “ Evolutionary game theory: temporal and spatial effects beyond replicator dynamics” Physics of Life Reviews 6, 208-249 (2009).
Abstract
Evolutionary game dynamics is one of the most fruitful frameworks for studying evolution in different disciplines, from Biology to Economics. Within this context, the approach of choice for many researchers is the so-called replicator equation, that describes mathematically the idea that those individuals performing better have more offspring and thus their frequency in the population grows. While very many interesting results have been obtained with this equation in the three decades elapsed since it was first proposed, it is important to realize the limits of its applicability. One particularly relevant issue in this respect is that of non-mean- field effects, that may arise from temporal fluctuations or from spatial correlations, both neglected in the replicator equation. This review discusses these temporal and spatial effects focusing on the non-trivial modifications they induce when compared to the outcome of replicator dynamics. Alongside this question, the hypothesis of linearity and its relation to the choice of the rule for strategy update is also analyzed. The discussion is presented in terms of the emergence of cooperation, as one of the current key problems in Biology and in other disciplines.

