Network Theory Approach
A powerfool tool for the study of Complex Systems
Networked systems are everywhere. The accumulated evidence that complex systems cannot be fully understood by studying only their isolated constituents, has given rise to the birth of a new scientific movement aimed at the study of complex networks. The expectancy is that understanding and modeling the structure of a complex network would lead to a better cottoning on its dynamical and functional behavior. Through network theory, we are able to test and demonstrate the innovative use of tools and methods that have been developed during the last few years and also support new methodologies in the analysis and design of complex systems. Thus, the findings and results obtained will deliver new and valuable insights in many scientific fields such as biological and social sciences.
Cooperative phenomena are essential in natural and manmade systems and have been the subject of intense research during the last decades using, among other approaches, the evolutionary game theory. It is well known that the dynamics of complex systems and their collective behavior strongly depend on several factors. When it comes to analyze cooperative behavior, aspects such as the specific game, the way in which strategies spread, the structure of the connections of interactions, etc., are key elements to understand how cooperation evolves. With the advent of complex networks, we could be able to thoroughly study the influence of the real contact patterns among agents in the emergence and survival of global cooperation as well as to develop new models to better understand the onset and evolution of cooperative behavior in biological and social systems.
Indeed, the fact that the underlying structure is believed to sustain cooperative behavior led to propose a mechanism known as «network reciprocity». However, whether this mechanism plays any role in human cooperation is, at least, not proven experimentally. See Experiments.
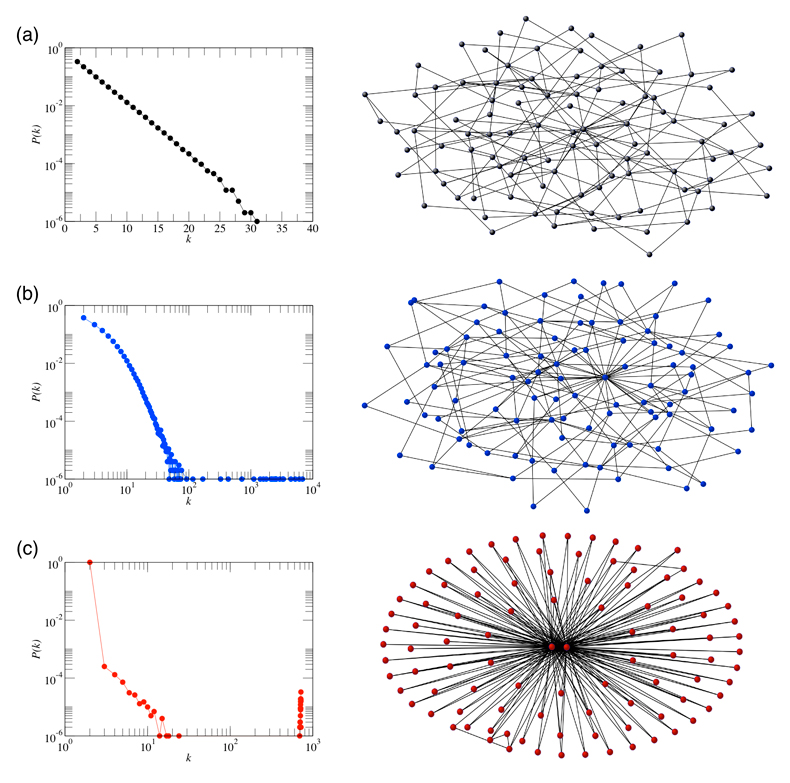
The figure below shows that the structure of a population could be shaped by its dynamics, in this case given by an evolutionary game. See the corresponding paper here.
For a comprehensive review on the structure and dynamics of complex networks and their applications, see:
PDF Version “Complex Networks: Structure and Dynamics“, Physics Reports 424, 175-308 (2006).
Abstract: Coupled biological and chemical systems, neural networks, social interacting species, the Internet and the World Wide Web, are only a few examples of systems composed by a large number of highly interconnected dynamical units. The first approach to capture the global properties of such systems is to model them as graphs whose nodes represent the dynamical units, and whose links stand for the interactions between them. On the one hand, scientists have to cope with structural issues, such as characterizing the topology of a complex wiring architecture, revealing the unifying principles that are at the basis of real networks, and developing models to mimic the growth of a network and reproduce its structural properties. On the other hand, many relevant questions arise when studying complex networks’ dynamics, such as learning how a large ensemble of dynamical systems that interact through a complex wiring topology can behave collectively. We review the major concepts and results recently achieved in the study of the structure and dynamics of complex networks, and summarize the relevant applications of these ideas in many different disciplines, ranging from nonlinear science to biology, from statistical mechanics to medicine and engineering.
Abstract: Coupled biological and chemical systems, neural networks, social interacting species, the Internet and the World Wide Web, are only a few examples of systems composed by a large number of highly interconnected dynamical units. The first approach to capture the global properties of such systems is to model them as graphs whose nodes represent the dynamical units, and whose links stand for the interactions between them. On the one hand, scientists have to cope with structural issues, such as characterizing the topology of a complex wiring architecture, revealing the unifying principles that are at the basis of real networks, and developing models to mimic the growth of a network and reproduce its structural properties. On the other hand, many relevant questions arise when studying complex networks’ dynamics, such as learning how a large ensemble of dynamical systems that interact through a complex wiring topology can behave collectively. We review the major concepts and results recently achieved in the study of the structure and dynamics of complex networks, and summarize the relevant applications of these ideas in many different disciplines, ranging from nonlinear science to biology, from statistical mechanics to medicine and engineering.